This article is on the Thermodynamics Notes Class 11 of Chemistry. The notes on Thermodynamics of class 11 chemistry have been prepared with great care keeping in mind the effectiveness of it for the students. This article provides the revision notes of the Thermodynamics chapter of Class 11 for the students so that they can give a quick glance of the chapter.
THERMODYNAMICS
Thermodynamics, as the word suggests, is the heat in motion. The systems related to the usage of heat for doing work. Every system was observed and accordingly, laws were framed for categorizing many such processes.
Thermodynamics is a Greek word which means flow of heat in physical and chemical reactions. Thermodynamics is a branch of science dealing with the study of different forms of energy and their interconversions.
TERMS USED IN THERMODYNAMICS
System, surroundings and Boundary
A thermodynamic system refers to the part of the universe which is under and the remaining portion of the universe constitutes the surroundings. The system and the surroundings are separated by real or imaginary boundaries. The system and the surroundings can interact across the boundary.
Types of systems
(i) Isolated system: This type of system does not allow the transfer of both matter and energy. Thermos flask is an example of an isolated system.
(ii) Closed system: This type of system allows transfer of energy as heat and work, but not of matter. For example, a closed teapot.
(iii) Open system: This type of system allows the transfer of both matter and energy. A hot cup of tea is an example of an open system.
State of a system and State Variables
Macroscopic properties such as pressure, temperature, volume, amount, etc. which determine the state of a system are referred to as state variables or state functions or thermodynamic parameters. The change in the state properties depends only upon the state of the system and independent of the path followed.
Thermodynamic processes
Thermodynamic processes can be isothermal (at constant temperature), adiabatic (completely insulated), isobaric (at constant pressure), isochoric (at constant volume), cyclic, reversible or irreversible.
(i) Isothermal process: In this process, the operation is done at a constant temperature. dT = 0 thus DU = 0 .
(ii) Adiabatic process: In this a process there is no exchange of heat takes place between the system and surroundings. The system is thermally isolated, i.e., dQ = 0.
(iii) Isobaric process: The pressure of the system remains constant throughout the process i.e., dP = 0.
(iv) Isochoric process: The volume of the system remains constant throughout the process, i.e., dV = 0.
(v) Cyclic process: When a system undergoes a series of changes and finally return to its initial state, it is termed a cyclic process. For a cyclic process dE = 0 and dH = 0.
(vi) Reversible process: A process which is carried out infinitesimally slowly, so that all change occurring in the direct process can be reversed and the system the surroundings remain in the state of equilibrium is said to be a reversible process. It is an ideal process.
(vii) Irreversible process: When a change is brought about rapidly and the system does not attain equilibrium is termed an irreversible process. The force which drives the reactant towards products is greater than opposing force used to carry the reverse process. Amount of entropy increases in an irreversible process.
Irreversible processes are spontaneous in nature. All natural processes are irreversible in nature
Internal energy
Internal energy (U) is the total energy within a system. It is the sum of all types of energies (chemical, electrical, mechanical or any other type) of the system and is a state function.
Change in internal energy (DU)
It is neither possible nor necessary to calculate the absolute value of internal energy of a system then, DU = Uf – Uin; DU is positive if Uf > Uin and negative if Uf < Uin.
Heat (q) and work (w)
The energy of a system may increase or decrease in several ways but two common ways are heat and work.
Heat is a form of energy. It flows from one system to another because of the difference in temperature between them. Heat flows from a higher temperature to lower temperature. Therefore, it is regarded as energy on the move.
Work is said to be performed if the point of application of force is displaced in the direction of the force. It is equal to the force multiplied by the displacement (distance through which the force acts).
ZEROTH LAW OF THERMODYNAMICS
It was introduced after the 1st and 2nd law and thus got its name.
The law states: If two systems are in equilibrium with a third system, they are also in thermal equilibrium with each other. If objects A and B are separately in thermal equilibrium with a third object C, then A and B are in thermal equilibrium with each other.
FIRST LAW OF THERMODYNAMICS
The increase in the internal energy of a thermodynamic system is equal to the amount of heat energy added to the system minus the work done by the system on the surroundings. When a system is changed from an initial state to the final state it undergoes a change in the internal energy from Ui to Uf. Thus, ∆E can be written as ∆U = Uf – Ui
The change in internal energy can be brought about in two ways.
(a) Either by allowing the heat to flow into the system (absorption) or out of the system (evolution).
(b) By doing work on the system or the work done by the system.
Therefore, Uf – Ui = q + w or ∆U = q + w
Therefore, we can state that the change in the internal energy of the system is equal to heat absorbed plus work done on the system.
OR
The change in internal energy of the system is equal to heat absorbed minus work done by the system.
OR
Energy is conserved; it can be neither created nor destroyed.
Therefore, it can be summarized as: dU = dq + dw
Or Mathematical statement: ∆U = q + w
∆Usystem = q + w;
∆Usurroundings = – q – w
⇒ Uuniverse = ∆Usystem + ∆Usurroundings = 0
Clausius statement of 1st law: The energy of the universe is conserved.
Work
Work is defined as a movement against force. It is a mode of energy transfer to or from a system with reference to surroundings.
Work: W = F.l , where F = Applied Force and l = Distance
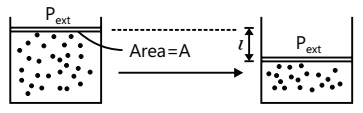
Mathematical Expression: If an object is displaced through a distance l against a force F, then the amount of work done is defined as expansion work.
Work associated with the change in volume of a system against external pressure is called mechanical work.
Mechanical Work (=W) = Pext (V2 – V1) = Pext ∆V
Where Pext =External pressure, ∆V =increase or decrease in volume.
Convention
‘-’ Sign is required when W>0 Positive work and ∆V<0. This indicates that Work is done ON the system BY the surroundings
‘+’ Sign is required when W<0 Negative work and ∆V>0. This indicates that Work is done BY the system ON the surroundings
If Pext is not constant, then we have to look at infinitesimal changes.
dw = – Pext dV (d means this is not an exact differential)
Integral w = – 1∫2 Pext dV (depends on the path)
A process which is carried out infinitesimally slowly, so that all change occurring in the direct process can be reversed and the system the surroundings remain in the state of equilibrium is said to be a reversible process. It is an ideal process. When a change is brought about rapidly and the system does not attain equilibrium is termed an irreversible process. The force which drives the reactant towards products is greater than opposing force used to carry the reverse process. Amount of entropy increases in an irreversible process.
Expansion of Ideal Gases
Isothermal Expansion
Isothermal Gas Expansion: In an isothermal gas expansion the temperature of the system remains constant throughout the process. Since internal energy depends on temperature, it follows that at constant temperature the total internal energy of the system remains constant. i.e ∆U = 0
According to first law thermodynamics,
∆Usystem = q + w; Since for isothermal expansion ∆U = 0 ; q = – w
Also ∆H = ∆U + ∆(nRT) since ∆U and ∆T are zero, Hence ∆H = 0
Gas (p1, v1, T) => gas (p2, v2, T) (∆T = 0)
Work done in the reversible isothermal expansion
The work done by the gas in each step of expansion can be given as
dw = – (Pext – dp)dV = – Pext .dV = – PdV
Total amount of work done by the isothermal reversible expansion ideal gas from volume V1 to volume V2 is,
Wrev = V1∫V2 PdV
For an ideal gas, P = nRT/V
So, w = nRT V1∫V2 dV/V
Integrating, w = – nRT loge V2/V1 = – 2.303nRT log V2/V1
At constant temperature, according to Boyle’s Law, w = – 2.303nRT log P1/P2
Work done for Isothermal Compression: It has the exactly same value as that of isothermal expansion but with opposite sign.
w = 2.303nRT log V1/V2 = w = 2.303nRT log P2/P1
Work done for Irreversible Isothermal Expansion
(a) Free expansion: In free expansion external work is zero thus work done is zero.
(b) Intermediate expansion:
W = V1∫V2 Pext x dV = – Pext (V2 – V1)
Maximum Work: Maximum work delivered to surroundings for isothermal gas expansion is obtained using a reversible path.
For ideal gas: Wrev = – V1∫V2 (nRT/V) dV = nRT ln P2/P1
Free Expansion
Adiabatic free expansion
(a) Expansion of gas in vacuum i.e. at zero external pressure, the system will give zero work.
(b) Thus, Wirr = 0
Wirr = 0
Q = 0
∆E = – Wirr = nCv (T2 – T1 )
∆H = nCp (T2 – T1 ) = 0
Considering an ideal gas, the above case is true. But, the final states of reversible and irreversible adiabatic transformations will be different. Thus, ∆E and ∆H will be different.
Enthalpy
Considering a system at constant pressure, the amount of heat which is released or absorbed is termed as Enthalpy. The change in enthalpy for a specific process is actually the change in internal energy associated with the changing volume.
H = U + PV
Enthalpy is a

and an extensive property.
Let a system at state-I be transformed to state – II at constant pressure condition H = U + PV
H2 – H1 = ∆H = (E2+ PV2) – (E1 + PV1)
= (E2- E1) + P (V2 – V1)
∆H= ∆E + P∆V
Also for an ideal gas PV = nRT PV1 = n1RT and PV2 = n2RT ⇒ P(V2 – V1) = ∆ngRT
When ∆ng = 0 ⇒ ∆H = ∆E
When ∆ng > 0 ⇒ ∆H > ∆E
When ∆ng < 0 ⇒ ∆H < ∆E
Also ∆E = qp – P∆V qp = ∆E + P∆V
And ∆H = qp (i.e. Enthalpy change = heat exchange at constant pressure condition)
Also ∆E = qv, ∆H = ∆E + P∆V, qp = qv + P∆V
Extensive and Intensive Properties
(i) Intensive properties: The properties that are independent of the quantity of matter or size of the system are called intensive properties. Its examples are pressure, temperature, density, specific heat, surface tension, refractive index, viscosity, etc.
(ii) Extensive properties: The properties which depend on the quantity of matter present in the system are called extensive properties. Its examples are total mass, volume, internal energy, enthalpy, entropy etc.
Heat Capacity
The flow or exchange of energy between the system and the surroundings which can induce a change in the temperature of the system and/or the surroundings is known as heat. Heat always flows from a high temperature to low temperature. It is expressed as q.
Heat absorbed or evolved, q = ms∆t
m = Mass of substance, s = Specific heat and ∆t = Temperature difference.
If heat is absorbed by the system, q= +ve
If heat is released by the system, q= -ve
Heat capacity is the amount of heat required to raise the temperature by one degree (usually expressed in Celsius or Kelvin). It is expressed in units of thermal energy per degree temperature. It is expressed as C.
Let dq be the amount of heat given to a system and the temperature of the system rises by dT.
Heat capacity= dq/dT
Relationship between Cp and Cv for an ideal gas
Two specific heats are defined for gases, one for constant volume (CV) and one for constant pressure (CP). For a constant volume process, the first law of thermodynamics gives:
Qv = CV ∆T = ∆U
For a constant pressure process, the first law of thermodynamics gives:
Qp = Cp ∆T = ∆H
The difference between CV and Cp can be derived for an ideal gas as:
For a mole of an ideal gas, ∆H = ∆U + ∆(pV)
= ∆U + ∆(RT)
= ∆U + R∆T
Therefore, ∆H = ∆U + R∆T
On putting the value of ∆H and ∆U, we have
Cp ∆T = Cv ∆T + R∆T
Cp = Cv + R
Cp – Cv = R
Cp/Cv = γ
For monoatomic gas, γ = 1.66; for diatomic gas, γ = 1.40; for triatomic gas, γ = 1.33.
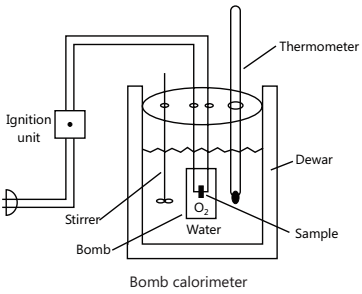
Measurement of ∆U:
It is done in a bomb calorimeter.
∆U = C x ∆t x M; where m is mass of substance taken, M is its molar mass, C is the heat capacity of the calorimeter and ∆t is the rise in temperature.
Measurement of ∆H:
The reaction is carried out in an insulated vessel (calorimeter) directly and rise or fall in temperature is noted down depending upon whether the reaction is exothermic or endothermic.
Enthalpy Change, ∆rH of a Reaction – Reaction enthalpy:
The enthalpy change accompanying a reaction is called reaction enthalpy.
∆rH = (sum of enthalpies of products) — (sum of enthalpies of reactants)
= ∑ ai Hproducts – ∑ bi Hreactants
where ai and bi is the stoichiometric coefficients of the products and reactants respectively.
Standard Enthalpy of Reaction
The standard enthalpy of reaction is related to bond enthalpies of the reactants and products in gas phase reactions as
∆rHo = ∑ bond enthalpiesreactants – ∑ bond enthalpiesproducts
Standard Enthalpy of Formation
The definition of the standard enthalpy of formation is the change in enthalpy when one mole of a substance, in the standard state of 1 atm of pressure and temperature of 298.15 K, is formed from its pure elements under the same conditions.
The equation for the standard enthalpy change of formation:
ΔHf reaction =∑ΔHf (products) – ∑ΔHf (Reactants)
The standard enthalpy change of formation is equal to the sum of the standard enthalpies of formation of the products subtracted by the sum of the standard enthalpies of formation of the reactants.
THERMOCHEMICAL EQUATIONS
A Thermochemical equation presents a chemical reaction stating the amount of heat released or absorbed during the process. A thermochemical equation gives:-
(a) The physical state or the phase of the reactants and the products using the symbols s, l, g or aq (aqueous).
(b) The allotropic form (if any) of the reactant.
(c) It tells whether a reaction proceeds with the evolution of heat or with the absorption of heat, i.e. heat change involved in the system. Heat changes of the system, the heat of reactant and product are represented by ∆H, HR and HP respectively.
Mathematically, ∆H = HP – HR
For Exothermic reactions, HR > HP or ∆H is negative.
For endothermic reactions, HP > HR or ∆H is positive.
Hess’s law of constant heat summation
If a reaction takes place in several steps then its standard reaction enthalpy is the sum of the standard enthalpies of the intermediate reactions into which the overall reaction may be divided at the same temperature.
∆rH = ∆rH1 + ∆rH2 + ∆rH3 …….
Enthalpy of Combustion
The standard enthalpy of combustion is the enthalpy change when one mole of a reactant completely burns in excess oxygen under standard thermodynamic conditions (although experimental values are usually obtained under different conditions and subsequently adjusted). It is measured using bomb calorimetry, and have units of energy (typically kJ).
Enthalpy of atomization ( ∆aH )
It is the enthalpy change (always positive) when one mole of a substance is completely dissociated into atoms in the gaseous state, under constant pressure and temperature condition.
For example, H2 (g)→ 2H (g) ; ∆fH=435.0kJ mol-1 CH4 (g)→ C (g) + 4H (g) ; ∆fH=1665kJ mol-1
Enthalpy of Solution
Enthalpy of solution of a substance is the enthalpy change when one mole of it dissolves in a specified amount of solvent.
∆solHo = ∆latticeHo + ∆hydHo
Enthalpy of a solution at infinite dilution is the enthalpy change observed on dissolving the substance in an infinite amount of solvent when the interactions between the ions are negligible.
Lattice enthalpy
Lattice enthalpy of an ionic compound is the enthalpy change which occurs when one mole of an ionic compound dissociates into its ions in the gaseous state. It is calculated by using the Born-Haber cycle e.g; in case of NaCl.
∆fHo (NaCl) = ∆subH(Na) + ½ ∆dissH(Cl2) + ∆ionH(Na)+ ∆egH(Cl) + ∆latticeH(NaCI)
Spontaneity
It can be defined as the process which takes place by itself or by initiation.
Entropy
Entropy (S) is a measure of the degree of randomness or disorder of the system. ∆S is related with q and T for a reversible reaction as:
∆S = qrev/T
∆Stotal = ∆Ssystem + ∆Ssurroundings > 0
∆Ssys = qsys, rev/T
Second law of thermodynamics:
For all the spontaneous processes, the total entropy change is positive.
Gibbs free energy (G) is the net energy available to do useful work.
G = H – TS
Gibbs-Helmholtz equation
∆G = ∆H – T∆S
∆G° = ∆H° – T∆S°
∆Go = -nFE°; where, Eo is standard emf of cell.
∆Go = -2.303RT log K; where, K is equilibrium constant.
Gibbs energy and spontaneity
∆G gives a criterion for spontaneity at constant pressure and temperature.
If ∆G < 0, process is spontaneous.
If ∆G > 0, process is non-spontaneous.
If ∆G = 0, process is in equilibrium.
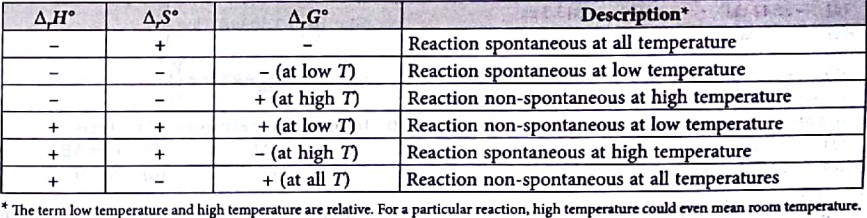
Effect of temperature on the spontaneity of reactions:
Third law of thermodynamics
The entropy of any pure crystalline substance approaches zero as the temperature approaches absolute zero.
This article has tried to highlight all the important points of Thermodynamics in the form of short notes for class 11 students in order to understand the basic concepts of the chapter. The notes on Thermodynamics have not only been prepared for class 11 but also for the different competitive exams such as iit jee, neet, etc.