This article is prepared about Chapter 5 States Of Matter Class 11 Notes of Chemistry. The notes on states of matter of class 11 chemistry have been prepared with great care keeping in mind the effectiveness of it for the students. This article provides the revision notes of chapter 5: States of Matter chapter of Class 11 Chemistry for the students so that they can give a quick glance of the chapter.
States of Matter
Matter can be defined as anything that occupies volume and has mass. Matter can be classified into three states – solid, liquid and gas. Plasma is regarded as the fourth state of matter, which exists only at very high temperatures (at interiors of stars, 107 K). At very high temperatures, all gases become ionized, which results in the formation of the fourth state of matter, the so-called plasma state. Matter can undergo a change in its physical state or chemical composition.
The major factor that is responsible for the different behaviour of solids, liquids and gases is the nature of the interaction between the particles(atoms, ions or molecules) and the effect of thermal energy on the movement of the particles.
Intermolecular forces
Intermolecular forces are the forces of attraction and repulsion between interacting particles (atoms and molecules) and are always much weaker than the chemical bonds that hold atoms of a molecule together.
VAN DER WAALS FORCES
Intermolecular attractions hold two or more molecules together. These are weakest chemical forces and can be of the following types.
Dipole-dipole attraction
These are electrostatic attractions between the oppositely charged ends of permanent dipoles. It exists between polar molecules and due to this force, gas can be liquefied.

Dipole-induced dipole attraction
It exists between polar and non-polar molecules.

Dispersion force or London forces
It is an Instantaneous dipole-Instantaneous induced dipole attraction.
It exists among the non-polar molecules like H2, O2, Cl2 etc. in solid or liquid states. Even in atoms or molecules which have no permanent dipole, instantaneous dipoles will arise as a result of momentary unbalances in electron distribution. London forces are extremely short range in action and the weakest of all attractive forces. The London forces increase rapidly with molecular weight, or more properly with the molecular volume and the number of polarizable electrons.
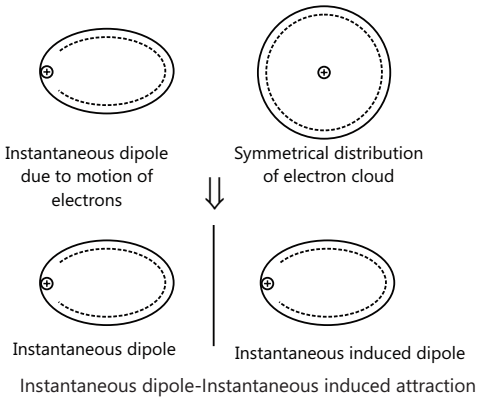
Hydrogen Bond
Nitrogen, oxygen and fluorine are the highly electronegative elements. When they are tied to a hydrogen atom to form a covalent bond, the electrons of the covalent bond are shifted towards the more electronegative atom. This partially, positively charges the hydrogen atom forming a bond with the other more electronegative atom. This bond is called a hydrogen bond and is weaker than a covalent bond. For example, in HF molecule, the hydrogen bond exists between the hydrogen atom of one molecule and fluorine atom of another molecule as given below :

Thus, hydrogen bond can be defined as the attractive force which binds the hydrogen atom of one molecule with the electronegative atom (F, O or N) of another molecule. Hydrogen bonding is said to be formed when slightly acidic hydrogen attached to a strongly electronegative atom such as F, N and O is held with weak electrostatic forces by the lone pair of electrons of the electronegative atom i.e. the strongly positive H and the strongly electronegative lone pair tend to line up and hold the molecules together. Other atoms with high electronegativities, such as Cl, can also form hydrogen bonds in strongly polar molecules such as chloroform, CHCl3.
Conditions required for H-bond :
(i) Molecule should have a more electronegative atom (F, O, N) linked to H-atom.
(ii) Size of the electronegative atom should be smaller.
(iii) A lone pair should be present on an electronegative atom.
Thermal energy
Thermal energy is the energy of a body arising from the motion of its atoms or molecules and is directly proportional to the temperature of the substance.
Intermolecular forces vs Thermal Interactions
Intermolecular forces tend to keep the molecule together but the thermal energy of molecules tends to keep them apart. Three states of matter are the result of a balance between intermolecular forces and the thermal energy of the molecules.
The Gaseous State
Characteristics of gases
(1) Gases or their mixtures are homogeneous in composition.
(2) Gases have very low density due to negligible intermolecular forces.
(3) Gases have infinite expansibility and high compressibility.
(4) Gases exert pressure.
(5) Gases possess high diffusibility.
(6) Gases do not have definite shape and volume like liquids.
(7) Gaseous molecules move very rapidly in all directions in a random manner i.e., gases have the highest kinetic energy.
(8) Gaseous molecules collide with one another and also with the walls of the container with perfectly elastic collisions.
(9) Gases can be liquefied if subjected to low temperatures (below critical) or high pressures.
(10) Thermal energy of gases >> molecular attraction.
(11) Gases undergo similar change with the change of temperature and pressure. In other words, gases obey certain laws known as gas laws.
GAS LAWS
Among the three common states of matter, the gaseous state is the simplest. The laws of gaseous behaviour are more uniform and better understood. The well-known laws of gaseous behaviour are the Boyle’s law, Charles’s law, Graham’s law and Avogadro’s law.
Boyle’s Law
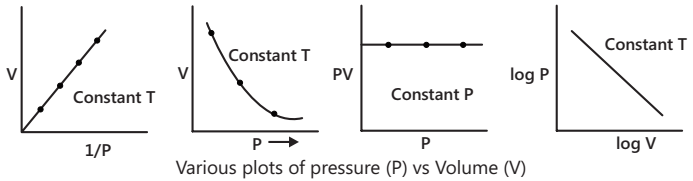
Boyle’s law states that at a constant temperature, the volume of a given mass of a gas is inversely proportional to pressure.
V ∝ 1/P (T and mass of gas constant); PV = constant
Log P + log V = constant
Charles’ Law
Charles’s law states that at constant pressure, the volume of a given mass of gas is directly proportional to its absolute temperature,
i.e. V ∝ T (P and m constant) ⇒ V = KT ⇒ V/T = constant = K
Also Read: Molecular explanation of Boyle’s and Charles’s Law

Gay-Lussac’s Law or Pressure-Temperature Law
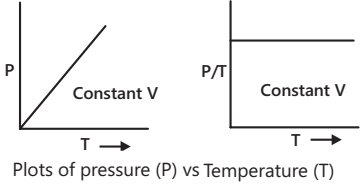
Gay-Lussac’s law states that at constant volume, the pressure of a given mass of gas is directly proportional to its absolute temperature, i.e. P ∝ T ( V and mass of gas constant).
P1/T1 = P2/T2 = Constant
Avogadro’s Law
Avogadro’s law states that equal volumes of all gases under similar conditions of temperature and pressure will contain an equal number of molecules or vice versa, i.e. V ∝ n (at constant T and P)
IDEAL GAS EQUATION
From the gas laws, we have found that V ∝ 1/P (Boyle’slaw); V ∝ T (Charles’ law); V ∝ n (Avogadro’slaw); and V ∝ nT/P ⇒ PV = nRT, where R = universal gas constant.
Hence, PV = nRT is the ideal gas equation.
Moreover,R= PV/nT
At STP, for 1 mole of gas
P = 1 atm; V = 22.4 L; T = 273 K; n = 1 mole
⇒R= 1 x 22.4/1 x 273 = 0.0821 L atm K–1 mol–1
R= (76 x 13.6 x 981)22400/1 x 273 = 8.314 × 107 erg K–1 mol–1 = 8.31 J K–1 mol–1; R= 1.99 calK–1mol–1
Combined Gas Law
P1V1/T1 = P2V2/T2
Relation of Density with Ideal Gas Equation
PV = nRT; N = Number of moles = amount of gas/Mol. wt of gas = w/M0
⇒PV= w/M0 × RT ⇒ PM0 = (w/V) RT = DRT, where D = Density of gas; PM0 = DRT
DALTON’S LAW OF PARTIAL PRESSURE
Statement: At a given temperature, the total pressure exerted by two or more non reacting gases occupying a definite volume is equal to the sum of the partial pressures of component gases.
PTotal= (nTotal RT)/V
Let nA moles of A, nB moles of B,etc., be the non-reacting gases present in a container of volume V at a constant
temperature.
PT= (nA + nB + nC + nD …..)RT/V = (nART)/V + (nBRT)V + (nCRT)/V + (nDRT)/V + … = PA+PB+PC+PD+….
Where PA, PB, etc., are the partial pressures of individual gases if they were present alone in the same container of
volume V (litres) and same constant temperature T.
The partial pressures can be calculated as follows:
PA is also equal to the mole fraction of a gas multiplied by the total pressure exerted by the mixture of gases.
PA= (nA/n) × PT = XAPT, where XA = Mole fraction of a gas
KINETIC THEORY OF GASES
The kinetic theory of gases (proposed by Bernoulli in 1738; developed by Clausius. Maxwell and Boltzmann) postulates the following:
(a) Gaseous molecules are considered to be point masses.
(b) The volume of a molecule of a gas is negligible as compared with the total volume of the gas.
(c) Gaseous molecules do not have appreciable attraction; hence, gases can be easily compressed and do not have a fixed shape and volume.
(d) Gaseous molecules collide with each other but their collisions are perfectly elastic, i.e. there is no net loss of energy.
Consider two molecules A and B with mass m. Their speeds are VA and VB, respectively. After the collision, let the new speeds to be VA’ and VB’, respectively. As the collisions are perfectly elastic,
Total energy before the collision – Total energy after the collision
½ MVA2 + ½ MVB2 = ½ MV’A2 + ½ MV’B2 ⇒ VA2 + VB2 = V’A2 + V’B2
(e) The average kinetic energy of a molecule is directly proportional to its temperature.
(f) There is no effect of gravity on the molecular motion.
(g) The pressure exerted is due to collisions with the wall of the container.
BEHAVIOUR OF REAL GASES – DEVIATIONS FROM IDEAL GAS BEHAVIOR
An ideal gas is a hypothetical gas whose pressure, volume and temperature behaviours are completely described by the ideal gas equation. Moreover, an ideal gas does not liquefy, but the case is exactly the opposite for a real gas, which can be analyzed by observing the deviation from an ideal gas.
Deviations From Ideal Gas Behavior
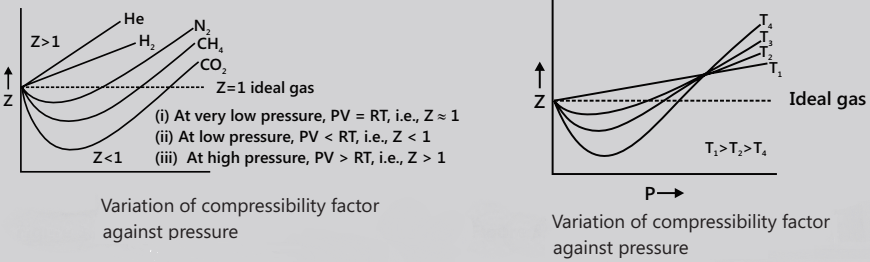
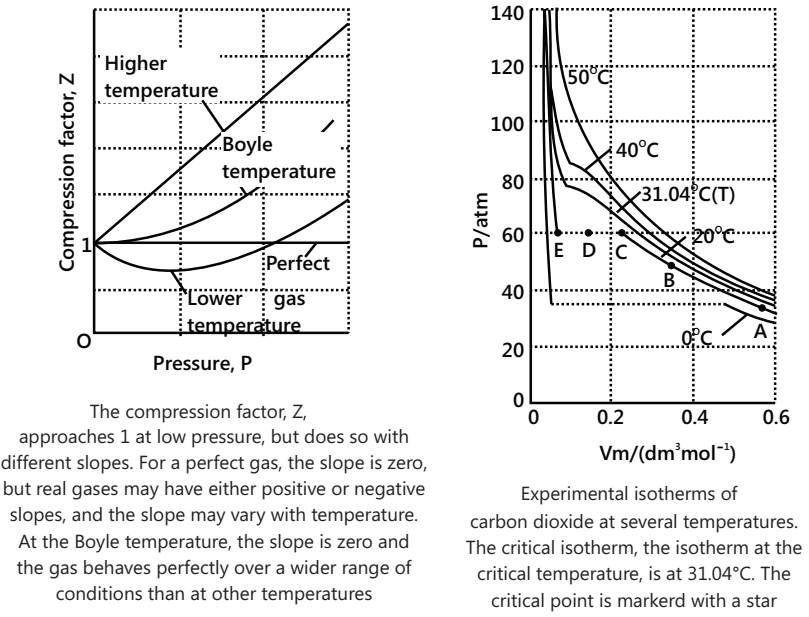
The deviations from the ideal gas behaviour are expressed in terms of compressibility factor (Z), where Z = PV/nRT = PV/RT (for 1 mole) = VM/VM ideal, where VM is the actual molar volume of gas.
Variation of Z with P and T
The values of Z exhibit both negative deviation (Z<1) and positive deviation (Z>1). Exceptional behaviour of H2 and He: For these gases, experimental studies have revealed that PV>RT, i.e. Z>1 or VM>22.4L at NTP. The deviation is more prominent at high Pand low T.
Real Gases
Van der Waals’ Equation – A Modification in Gas Equation
Van der Waals pointed out that Maxwell had made two wrong assumptions in his kinetic theory of gases, which led to wrong results. According to van der Waals’, it is not advisable to assume the following:
(a) The volume occupied by the gaseous molecules is negligible as compared with the total volume of the gas at all conditions. Thus, van der Waals pointed out the two corrections in the gas equation.
(b) The forces of attraction among gaseous molecules are negligible at all conditions.
Volume Correction
Excluded volume for one molecule in motion= 4v
∴ Excluded volume for ‘N’ molecules in motion= 4N.v
∴ Effective or excluded or co-volume of 1 mole = 4N.v = b
Real or compressible or ideal volume of gas
= Actual volume of container – volume occupied by N molecules in motion
∴ Real volume of a gas = (V-b)
Pressure Correction
Real pressure of a gas = Pressure developed due to collisions + Pressure loss due to attraction = P + P’
(Since in gases, a uniform distribution of molecules occurs)
Hence, P’∝ n2 ∝ d2 ∝ 1/V2, where d is the density of a gas and V is volume or P’= a/V2, where a is van der Waals’
constant of attraction.
The gas equation after the second correction is [P + (a/V2)] [V–b]=RT.
CRITICAL PHENOMENON AND LIQUEFACTION OF GASES
The mathematical definition of the critical point is given by the following equation:
(∂p/∂V)T = 0 (∂2p/∂V2)T = 0
The critical isotherm on a p-V diagram has a point of inflection. Equations constitute a set of two equations in two unknowns, V and T.One can test to see whether an approximate equation of state gives a critical point by calculating these two derivatives for the equation of state and trying to solve the pair of equations. If a solution exists (T and V are neither zero nor infinity), then we say that the equation of state has a critical point.
The van der Waals’ equation of state is still an approximate equation of state and does not exactly represent any real gas. It has, however, some of the features of a real gas and is therefore used as the next best approximation to a real gas.Wewillderivethermodynamicrelationships(equations) using the ideal gas approximation. We can re-derive some of these equations using the van der Walls’ equation of state to see how these relationships are affected by gas non-ideality. Hence, the conclusion is as follows:
Critical Temperature: It is defined as the temperature above which gases can never be liquefied; however, the
pressure applied may be high.
Tc = 8a/27Rb
Critical Pressure: The pressure just required to liquefy a gas at critical temperature is known as critical pressure.
Pc = a/27b2
Critical Volume: The volume of a gas at the critical temperature and critical pressure is known as critical volume.
Vc =3b
Boyle Temperature
As already mentioned, the temperature at which a real gas obeys Boyle’s law is called the Boyle temperature, TB. It
is represented by the expression TB=a/bR.
Hydrogen and helium show heating effect on adiabatic expansion (Joule-Thomson effect) since their inversion
temperatures are low.
The Liquid State
Learn More About the Properties of Liquid States of Matter
Surface Tension
The surface tension of a liquid is defined as the force acting at right angles to the surface along a length of one centimetre of the surface. Surface tension is represented by the Greek letter gamma,γ. Owing to surface tension, molecules tend to leave the surface, i.e.the surface of the liquid tends to contract to the smallest possible area for given volume of the liquid. Further, for a given volume of liquid, a sphere has the minimum surface area, which explains why the drops of liquid are spherical. Hence, it is apparent that in order to increase its surface area, force must be exerted to overcome the surface tension. In other words, work has to be done to increase the surface area.
Hence, the surface tension of a liquid is defined as the work (energy) required to expand the surface of a liquid by unit area. Mathematically, surface tension=work done/change in the area. Therefore, the surface tension of a liquid may also be defined as the force in dynes necessary to rupture its surface along a length of one centimetre. In SI units, surface tension is defined as the force in Newton required to rupture a length of 1 meter of the surface of a liquid. Hence, the units of surface tension are dyne per cm (or Newton per meter in the SI system).
Variation with Temperature
The surface tension of a liquid decreases with an increase of temperature and becomes zero at its critical temperature (where the surface of separation between the liquid and its vapour disappears). The decrease in surface tension with an increase of temperature is due to the fact that with an increase of temperature, the kinetic energy of the molecule (and hence the speed of molecules) increases and hence the intermolecular force of attraction decreases.
Viscosity of Gases
Viscosity is defined as the internal resistance that one part of a fluid offers to the flow of another part of the fluid. Similar to liquids, gases also show viscous behaviour. For gases, we generally assume planes at a distance of the mean free path.
F = ηA(du/dz) where, F is the force required to maintain the flow of layers, A is the area of contact, (du/dz) is velocity gradient (the change in velocity with distance) and η is coefficient of viscosity. SI unit of viscosity coefficient is N s m-2.
The coefficient of viscosity(η) is given by the expression
η = 5/16 σ2 (mkT/π)1/2
where k is the Boltzmann constant equal to R/N, η and m are the diameter and mass of the molecule, respectively. Reciprocal of η gives fluidity. The variation of σ with pressure and temperature gives the nature of the intermolecular forces in the gas. The unit of viscosity is poise (dyne cm–2 s)in cgs and Pascal-second (Pas) or Newton second per square meter (Nsm–2) in SI units. The viscosity of gases, unlike for liquids, increases with an increasing temperature and is independent of pressure.
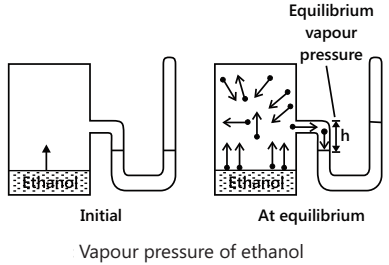
Vapour Pressure
The movement of molecules from the liquid phase into the gas phase (i.e. evaporation) goes on continuously. If the surface over the liquid is covered, the molecules in the vapour phase return after the collision with the covered area and, thus, strike the liquid surface and stick there. Furthermore, as the number of the gas-phase molecules increases, the probability increases that a molecule in the gas phase will strike the liquid surface and stick there. This phenomenon is known as condensation.
The rate of evaporation remains constant with time, whereas the rate of condensation increases with time. Eventually, the two attain equilibrium. The number of molecules returning to the liquid exactly equals the number of molecules escaping from it. The number of molecules in the gas phase then attains a steady value and the pressure of the vapours at this stage becomes constant and is usually referred to as vapour pressure.
(i) Nature of Liquids: Liquids have different magnitudes of intermolecular attractive forces and, therefore, have different vapour pressures. Liquids with higher intermolecular attractive forces have a lesser tendency for evaporation and thereby possess lower vapour pressure.
(ii) Temperature: As the temperature of liquid increases, the molecules move more energetically and can, therefore, escape more readily from their neighbours. Hence, the vapour pressure of every liquid increase as the temperature increases.
Conclusion
This article has basically tried to highlight the two states of matter (Gaseous and Liquid state) in the form of short revision notes of chapter 5 for class 11 students in order to understand the basic concepts of the chapter. The notes on states of matter have been prepared for both class 11 as well as for the different competitive exams such as IIT jee, neet, etc.