Lens Maker Formula Derivation With Diagram

In this article, we will be learning about the Lens Maker Formula which is also included in the syllabus of Physics in Class 12. We will first begin with the Definition, followed by some assumptions that are made to derive the lens maker formula. We will then go through the Sign Conventions used. Then we will derive Lens Maker Formula: derive lens maker formula for convex lenses and lens maker formula for concave lenses with diagrams.

The formula giving the relation between the focal length (f) of the lens, the refractive index of the material of the lens (n) and the radii of curvature of its surface (R₁ & R₂) is known as Lens maker formula.

The manufacturers of the lenses use this relation to design the lens of a given focal length and hence it is called so.

Assumptions made to derive Lens maker formula

(i) The lens is thin and all the distances are measured from the optical centre of the lens.

(ii) The aperture of the lens is small.

(iii) The object is a point object and lies on the principal axis.

(iv) The angle made by incident ray and refracted ray with the principal axis are small.

New Cartesian Sign Conventions

(i) All the distances are measured from the optical centre of the lens.

(ii) Distances measured in the direction of the propagation of incident light are taken as positive while the distances measured in the direction opposite to the direction of propagation of incident light are taken as negative.

Derivation of Lens Maker Formula for Convex lens

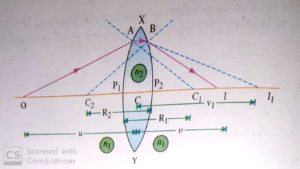
Consider a lens made of a material of absolute refractive index n₂. This lens is placed in a medium of absolute refractive index n₁ (n₁ < n₂ ). This lens is bounded by two spherical refracting surfaces XP₁Y and XP₂Y. C₁ and C₂ be their centres of curvature and R₁ and R₂ be their radii of curvature respectively. C is the optical centre of the lens.

STEP I. Refraction at Surface XP₁Y

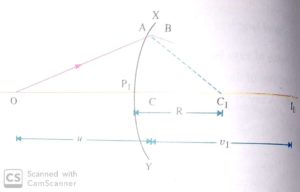
Let O be a point object lying in the rarer medium on the principal axis of the refracting surface XP₁Y. The incident ray OA after refraction at A bends towards the normal AC₁ and meets the principal axis at I₁ if the second surface XP₂Y were not present. So I₁ is the real image of the object O.

Since object lies in the rarer medium, so we have

– n₁/u + n₂/v₁ = n₂ – n₁/R₁      ……(i)

STEP 2. Refraction at Surface XP₂Y

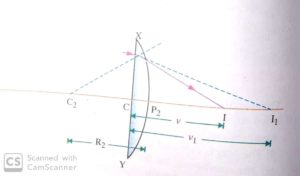
In fact, the ray AB refracted by the first surface XP₁Y is refracted at B by the second surface XP₂Y and it finally meets the principal axis at I. The point I₁ acts as a virtual object placed in the denser medium for the spherical surface XP₂Y. Now it is the situation, when the object is placed in the denser medium and image is formed in the rarer medium.

– n₂/v₁ + n₁/v= n₁ – n₂/R₂

or                                               – n₂/v₁ + n₁/v= – (n₂ – n₁)/R₂

– n₁/u + n₁/v = (n₂ – n₁) (1/R₁ – 1/R₂)

or                                              – 1/u + 1/v = (n₂/n₁ – 1) (1/R₁ – 1/R₂)

But n₂/n₁ = n, relative refractive index of the lens w.r.t. the rarer medium.

– 1/u + 1/v = (n – 1) (1/R₁ – 1/R₂)

If the object is at infinity, the image is formed at the principal focus of the lens.

Hence eqn. (vii) becomes

– 1/∞ + 1/f = (n – 1) (1/R₁ – 1/R₂)

or                                             1/f = (n – 1) (1/R₁ – 1/R₂)

Eqn. (viii) represents Lens maker formula.

Derivation of Lens Maker Formula for Concave Lens

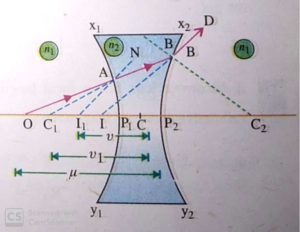
Let a concave lens have two spherical surfaces X₁P₁Y₁ and X₂P₂Y₂ having radius of curvature as R₁ and R₂ respectively.

STEP I. Refraction at X₁P₁Y₁

Let O be a point object lying in the rarer medium on the principal axis of the refracting surface X₁P₁Y₁. The incident ray OA after refraction at A bends towards the normal NC₁ and travel along AB. It appears to come from point  I₁ if the second surface X₂P₂Y₂ were not present. So I₁ is the virtual image of the object O.

So object lies in the rarer med1um, so we have

– n₁/u + n₂/v = n₂ – n₁/R

Here v = v₁ and R = R₁

∴                                                         – n₁/u + n₂/v₁ = n₂ – n₁/R₁      ……(i)

STEP 2. Refraction at X₂P₂Y₂

Ray AB inside the lens will stiffer another refraction at surface X₂P₂Y₂. After refracting from surface X₂P₂Y₂, the ray travels along BD and appears to come from the point I. So, I is the final virtual image of the object O. Point I₁ acts as the virtual object placed in the denser medium for the surface X₂P₂Y₂.

– n₂/u + n₁/v = n₁ – n₂/R

Here u = v₁ and R = R₂

∴                                                        – n₂/v₁ + n₁/v = n₂ – n₁/- R₂

STEP 3. Adding Eqs. (i) and (ii), we get

– n₁/u + n₁/v = (n₂ – n₁) (1/R₁ – 1/R₂)

or                                                           1/v – 1/u = (n₂/n₁ – 1) (1/R₁ – 1/R₂)

or                                                           1/v – 1/u = (n – 1) (1/R₁ – 1/R₂)                               (n2/n₁ = n)

For u = infinity, the image is formed at principal focus so v = f  (the focal length of the lens).

Then                                                    1/f – 1/∞ = (n – 1) (1/R₁ – 1/R₂)

or                                                               1/f = (n – 1) (1/R₁ – 1/R₂)