This article is on the Electrochemistry Class 12 Notes of Chemistry. The notes on the electrochemistry of class 12 chemistry have been prepared with great care keeping in mind the effectiveness of it for the students. This article provides the revision notes of the electrochemistry chapter of Class 12 Chemistry for the students so that they can give a quick glance of the chapter.
The entire chapter of electrochemistry has been divided into two articles. The first article includes the Electrochemical cell, Electrolytic cell, Nernst equation, Conductance, Types of electrolytes and Kohlrausch Law. The second article is on Electrolysis, Batteries, Fuel Cells and Corrosion.
Electrochemical Cell, Electrolytic Cell and Nernst Equation:
Electrochemistry is the study of spontaneous chemical reactions that lead to the production of electricity from the energy released and the use of it to bring about non-spontaneous chemical transformations.
In a redox reaction, one substance loses electrons and another substance gains electrons. In this, the transfer of electrons is the reason for the electric current.
There are two types of cells
1. Electrochemical Cell:
An electrochemical cell is a system or arrangement which consists of two metallic electrodes dipped in the same or different electrolytic solutions and joined by a salt bridge. In this cell, the chemical energy of the redox reaction is converted into electrical energy.
Galvanic Cell:
A galvanic cell is an electrochemical cell in which a spontaneous redox reaction converts the chemical energy of into electrical energy. In a galvanic cell, oxidation occurs at the anode and is the negative plate whereas Reduction occurs at the cathode and is the positive plate.
The two half-cell reactions are
(i) Cu2+ + 2e– —> Cu (reduction half-reaction)
(ii) Zn(s) –> Zn2+ + 2e– (oxidation half-reaction)
Daniell Cell: It is an improvement of the galvanic cell to solve the problem of polarisation which occurs with the galvanic cell.

In Daniell cell, the following reaction occurs
Zn (s) + Cu2+ (aq) —-> Cu(s) + Zn2+ (aq)
A cell is represented as
Zn I Zn2+ (C1) II Cu2+ (C2) I Cu
2. Electrolytic Cell:
If an external opposite potential is applied in the cell and is increased slowly, the reaction continues to take place till the opposing voltage reaches the value 1.1 V when the reaction stops altogether and no current flows through the cell. Any further increase in the external potential starts the reaction again but in the opposite direction. It now functions as an electrolytic cell. In an electrolytic cell, oxidation occurs at the anode but it is a positive plate and reduction occurs at the cathode, which is a negative plate.
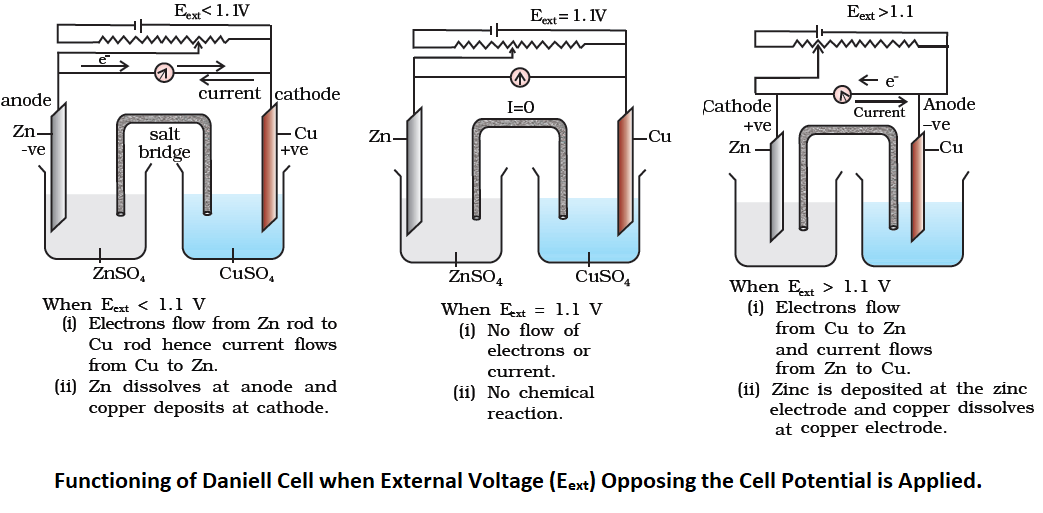
Note: Electrochemical or voltaic (galvanic) cells produce electricity as a result of chemical reactions, while in electrolytic cells, electricity is used to produce a non-spontaneous chemical change.
Standard Electrode Potential:
Electrode potential (E) in a given state is defined as the potential difference between the metal and the metal ion in which the electrode is dipped. When the concentrations and the pressure of all the species involved in a half-cell is unity in their standard state then the electrode potential is known as the standard electrode potential (E°) of the cell. According to the international convention, standard reduction potentials are now known as standard electrode potentials.
Electrode potential is dependent on the temperature and concentration of the ion involved.
Cell Potential:
The potential difference between the two half-cells is called the cell potential. It is given by the following formula,
E°cell = E°cathode — E°anode or E° right — E° left
Electromotive Force:
It (emf) is the potential difference when no current is drawn from the system. It is measured in volts (V).
For standard hydrogen electrode, E°SHE = 0.00 V. SHE and calomel electrode are used as reference half-cells.
Standard Hydrogen Electrode:
Half-cell or Standard Hydrogen Electrode (SHE) is Pt (s) I H2(g) 1 atm l H+ (aq). It is assigned to 0 potential at all temperatures.
H+ (aq) + e– —> 1/2 H2 (g)
The standard hydrogen electrode consists of a Pt electrode coated with platinum black which is dipped in an acidic solution and pure hydrogen gas is bubbled continuously through it. The concentration of hydrogen is maintained at unity both the reduced and oxidised forms.
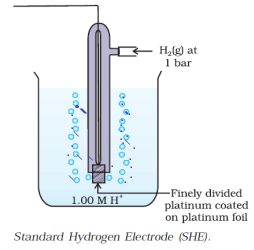
Note:
■ A metal having negative reduction potential is a stronger reducing agent than H2 and a metal having positive reduction potential is a weaker reducing agent than H2.
■ Hydrogen ions cannot oxidise Cu (or hydrogen gas con reduce copper ion) as it has a positive value of standard electrode potential, that’s the reason, Cu does not dissolve in HCl.
Nernst Equation:
Nernst equation gives the relation between electrode potential and the concentration of metal ions.
Mn+ + ne– —–> M
Ecell = E°cell – 2.303 RT/nF log[M]/ [Mn+] = E° – 0.059/n log 1/[Mn+]
For a voltaic cell, Zn I Zn2+ (C1) I I Cu2+ (C2) I Cu
Ecell = E°cell – 0.059/n log[C1 ]/[C2]
Equilibrium Constant from Nernst Equation:
Relationship between equilibrium constant and standard potential of the cell
Ecell = E°cell – 2.303RT/nF log Kc (where, Kc is equilibrium constant)
At equilibrium, Ecell = 0
E°cell = 2.303RT/nF logKc = 0.059/n log Kc
Electrochemical Cell and Gibbs Energy of the Reaction:
The charge has to be passed reversibly in order to obtain maximum work from a galvanic cell. The reversible work done by a galvanic cell is equal to decrease in its Gibbs energy.
Therefore, – ∆G° = maximum work = nFE°; ∆G° = -nFE°. If E°cell is positive, ∆G° = negative, cell will work. If E°cell is negative, ∆G° = positive, cell will not work.
Thus, from the measurement of E°cell we can obtain an important thermodynamic quantity, ∆rG°, standard Gibbs energy of the reaction. From the latter, we can calculate the equilibrium constant by the equation.
∆rG° = – RT lnK
Conductance of Electrolytic Solution:
Before introducing the subject of the conductance of electricity through electrolytic solutions, we must know about the electrical resistance.
Conductivity of Electrolytic Solution:
Resistance:
Every substance offers resistance to the flow of electricity to a small or large V extent. Resistance, R = V/I where V is voltage and I is current. SI unit of resistance is ohm (Ω). The electrical resistance R of any conductor is directly proportional to its length (l) and inversely proportional to its area of cross-section, (A), i.e., R α l/A or R= ρ l/A where ρ is called resistivity or specific resistance of the object.
Resistivity:
It can be defined as the resistance offered by a substance of 1 m length with an area of cross-section equal to 1 m2. SI unit of ρ is ohm-metre (Ω-m).
Conductance:
The power of the electrolyte with which current flows easily through a conductor is known as its conductance. It is inverse of resistance, i.e., conductance, G = 1/R = A/ρl =κ A/l . SI unit of conductance is Siemens (S) or ohm-1.
Conductivity:
The inverse of resistivity is called the conductivity (or specific conductance). Therefore, conductivity, κ = 1/ρ. SI unit of conductivity is S m-1 but quite often, it is expressed in S cm-1. It always decreases with the decrease in concentration for weak and strong electrolytes.
Note: Superconductors are said to have infinitive conductivity or zero resistivity.
Metallic Conductance:
Metallic or electronic conductance is due to the movement of electrons. The electronic conductance depends on
(i) the structure of the metal
(ii) the no of valence electrons per atom
(iii) temperature
(iv) nature of the metal
Electrolytic or Ionic Conductance:
The electrolytic or ionic conductance is the conductance of electricity by ions present in the solutions. The conductivity of electrolytic (ionic) solutions depends on
(i) the nature of the electrolyte added
(ii) temperature
(iii) concentration of the electrolyte
(iv) size of the ions produced and their solvation
(v) the nature of the solvent and its viscosity
Measurement of the Conductivity of Ionic Solutions:
The resistance of a conductor can be measured using Wheatstone bridge. The resistance of an electrolyte is measured by using a conductivity cell which has two platinum electrodes coated with platinum black. The area of cross-section of these electrodes is A and they are separated by distance l. Thus, the resistance of the column contained electrolytic solution between the electrodes is given by
R =ρ l/A or R = 1/κ x l/ A
Cell Constant:
The quantity, l/A is called cell constant (G ). The cell constant is given by, G =l/A = R x κ. SI unit of cell constant is m-1.
Molar Conductivity:
It is defined as the conducting power of the ions present in the solution produced by 1 mole of the electrolyte kept one centimetre apart.
Thus, molar conductance, Λm = κ x 1000/Molarity
It increases with the decrease in concentration (or increase in dilution). Its unit is S m2 mol-1 or S cm2 mol-1.
1 Sm2 mol-1 =104 S cm2 mol-1
1 Scm2 mol-1 =10-4 S m2 mol-1
When C —> 0, Λm = Λm0, i.e., when concentration approaches zero, the molar conductivity reaches a limiting value known as limiting molar conductivity (Λm0).
Types of Electrolytes:
There are two types of electrolytes
Strong Electrolytes:
The electrolytes which dissociate completely into ions are called strong electrolytes, e.g., NaCl, NaOH, etc. Strong electrolytes practically completely dissociate at all concentrations. For strong electrolytes, Λm increases slowly with dilution. This can be represented by the equation, Debye-Huckel-Onsager equation.
Λm = Λm0 – A√C
Weak Electrolytes:
The electrolytes which do not ionize completely in aqueous as well as in molten states are called weak electrolytes, e.g., H2CO3, CH3COOH, etc. A weak electrolyte like acetic acid is not completely dissociated at all concentrations. With dilution, the degree of dissociation increases, resulting in an increase in the number of ions. In such cases, the value of Λm0 increases steeply on dilution, especially near the lower concentrations and therefore it cannot be obtained by the assumption of Λm to zero concentration. At infinite dilution (i.e., concentration C –> zero), electrolyte dissociates completely (α =1). The conductivity of the solution is so low at such a low concentrations that it cannot be measured accurately. Therefore, in the case of weak electrolytes, the conductivity is obtained by using the Kohlrausch law of independent migration of ions. For a weak electrolyte, if Ka is dissociation constant, then
Ka =Cα2/1-α = C λm2 / λm0 (λm0 – λm)
The variation in Λm with concentration is different for strong and weak electrolytes and is shown in the figure below.
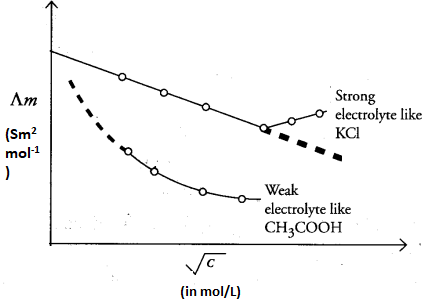
Kohlrausch Law of Independent Migration of Ions:
It states that at infinite dilution, the limiting molar conductivity of an electrolyte can be represented as the sum of the individual contribution of the anions and cations of the electrolyte. If on dissociation, an electrolyte gives v+ cations and v– anions, then its limiting molar conductivity is given by
Λm0 = ν+ λ+0 + ν–λ–0
where, λ+0 and λ–0 are the limiting molar conductivities of the cation and anion respectively and v+ and v– are the number of cations and anions respectively, at infinite dilution. The ratio of molar conductivity at any concentration to the molar conductivity at Infinite Acm dilution (limiting molar conductivity) is known as the degree of dissociation (α), i.e., α = Λmc / Λm0, where, Λmc is molar conductance at concentration C and Λm0 is molar conductance at infinite dilution.
Note: For sparingly soluble salts, Λm = κ x 1000 / Solubility (in mol L-1 )
This article has tried to highlight the basic concepts, terms related to electrochemistry in the form of short revision notes for class 12 students in order to understand the chapter easily. The notes on electrochemistry (Part 2) for class 12 has been given below.
Also Read: Electrochemistry Part 2 (Electrolysis, Batteries, Fuel Cells and Corrosion)