EAN Rule – Effective Atomic Number Rule

The 18-electron rule is sometimes referred to as the effective atomic number rule or EAN rule.

What is EAN rule with example?

The sum of the electrons on the metal plus the electrons donated from the ligands was called the effective atomic number (EAN), and when it was equal to 36 (Kr), 54 (Xe) and 86 (Rn), the EAN rule is said to be obeyed.

Key points: Six σ-bonding interactions are possible in an octahedral complex and, when π acceptor ligands are present, bonding combinations can be made with the three orbitals of the t2g set, leading to nine bonding MOs, and space for a total of 18 electrons.

In the 1920s, N.V. Sidgwick recognized that the metal atom in a simple metal carbonyl, such as [Ni(CO)4], has the same valence electron count (18) as the noble gas that terminates the long period to which the metal belongs. Sidgwick coined the term ‘inert gas rule’ for this indication of stability, but it is now usually referred to as the 18-electron rule or EAN Rule.

It becomes readily apparent, however, that the 18-electron rule is not as uniformly obeyed for d-block organometallic compounds as the octet rule is obeyed for compounds of Period 2 elements and we need to look more closely at the bonding to establish the reasons for the stability of both the compounds that have the 18-electron configurations and those that do not.

The rule is based on the fact that the valence shells of transition metals consist of nine valence orbitals (one s orbitals, three p orbitals and five d orbitals), which collectively can accommodate 18 electrons as either bonding or nonbonding electron pairs. This means that the combination of these nine A.O.s with ligand orbitals creates nine M.O.s that are either metal-ligand bonding or non-bonding.

Which does not obey EAN rule?

Ligands (donor-acceptor ligands) like carbonyls, carbenes, arenes, isonitriles, etc. forms complexes that tend to follow the EAN rule or the 18 electron rule.

Because the rule is obeyed with rather high frequency by organometallic compounds, especially those having carbonyl and nitrosyl ligands (π acceptor ligands), it has considerable usefulness as a tool for predicting formulas of stable compounds.

18 Electron Rule in Octahedral Complexes

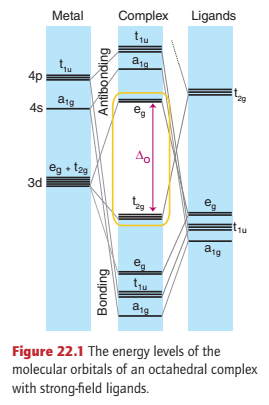
Figure 22.1 shows the energy levels that arise when a strong-field ligand such as carbon monoxide bonds to a d-metal atom.

Carbon monoxide is a strong-field ligand, even though it is a poor σ donor because it can use its empty π* orbitals to act as a good π acceptor. In this picture of the bonding, the t2g orbitals of the metal atom are no longer nonbonding, as they would be in the absence of π interactions, but are bonding.

The energy-level diagram shows six bonding MOs that result from the ligand–metal σ interactions, and three bonding MOs that result from π interactions. Thus up to 18 electrons can be accommodated in the nine bonding MOs.

Compounds that have this configuration are remarkably stable; for instance, the 18-electron [Cr(CO)6] is a colourless, air-stable compound.

An indication of the size of the HOMO-LUMO gap (ΔO) can be gained from a consideration of its lack of colour, which results from a lack of any electronic transitions in the visible region of the spectrum; that is, ΔO is so large that such transitions are shifted to the UV.

The only way to accommodate more than 18 valence electrons in an octahedral complex with strong-field ligands is to use an antibonding orbital. As a result, such complexes are unstable, being particularly prone to electron loss and acting as reducing agents.

Compounds with fewer than 18 electrons will not necessarily be very unstable. However, such complexes will find it energetically favourable to acquire extra electrons by reaction and so populate their bonding MOs fully.

The bonding characteristic of the carbonyl ligand is replicated with other ligands, which are often poor σ donors but good π acceptors. Hence, octahedral organometallic compounds are most stable when they have a total of 18 valence electrons around their central metal ion.

How do I calculate effective atomic number of coordinate compounds?

Q: Do (a) [IrBr2(CH3)(CO)(PPh3)2] and (b) [Cr(η5-C5H5)(η6-C6H6)] obey the 18-electron rule?

Answer

(a) We start with the Ir atom (Group 9), which has nine valence electrons, then add in the electrons from the two Br atoms and the CH3 group (each is a one-electron donor) and finally add in the electrons from the CO and PPh3 (both are two-electron donors). Thus, the number of valence electrons on the metal atom is 9+ (3×1) + (3×2) =18.

(b) In a similar fashion, the Cr atom (Group 6) has six valence electrons, the η5-C5H5 ligand donates five electrons, and the η6-C6H6 ligand donates six, so the number of metal valence electrons is 6+5 + 6=17. This complex does not obey the 18-electron rule and is not stable. A related but stable 18-electron compound is [Cr(η6-C6H6)2].

Problem on Effective Atomic Number Rule

Self-test:  Is [Mo(CO)7] likely to be stable?

Assign the oxidation number and count the valence electrons on the metal atom in

(a) [IrBr2(CH3)(CO)(PPh3)2], (b) [Cr(η5-C5H5)(η6-C6H6)], and (c) [Mn(CO)5]-.

Answer

(a) We treat the two Br groups and the CH3 as three singly negatively charged two-electron donors and the CO and the two PPh3 ligands as three two-electron donors, providing 12 electrons in all. Because the complex is neutral overall, the Group 9 Ir atom must have a charge of +3 (that is, have oxidation number +3) to balance the charge of the three anionic ligands, and thus contributes 9 -3 = 6 electrons. This analysis gives a total of 18 electrons for the Ir(III) complex.

(b) We treat the η5-C5H5 ligand as C5H5- and thus it donates six electrons, with the η6-C6H6 ligand donating a further six. To maintain neutrality, the Group 6 Cr atom must have a charge of +1 (and an oxidation number of +1) and contributes 6- 1 =5 electrons. The total number of metal electrons is 12 + 5 =17 for a Cr(I) complex. As noted before, this complex does not obey the 18-electron rule and is unlikely to be stable.

(c) We treat each CO ligand as neutral and contributing two electrons, giving 10 electrons. The overall charge of the complex is -1; because all the ligands are neutral, we consider this charge to reside formally on the metal atom, giving it an oxidation number of -1. The Group 7 Mn atom thus contributes 7+ 1 electrons, giving a total of 18 for a Mn(-1) complex.

Self-test:  What is the electron count for, and oxidation number of, platinum in the anion of Zeise’s salt, [Pt(CH2=CH2)Cl3]- ? Treat CH2=CH2 as a neutral two-electron donor.