All molecules can be described in terms of their symmetry, even if it is only to say they have none. Molecules or any other objects may contain symmetry elements such as mirror planes, axes of rotation, and inversion centres. The actual reflection, rotation, or inversion are called symmetry operations.

To contain a given symmetry element, a molecule must have exactly the same appearance after the operation as before.

Before proceeding into the details of the topic, we must know what symmetry means and what symmetry operations refer to.

What is a symmetry?

A molecule has symmetry means that certain parts of the molecule can be interchanged with others without altering either their identity or the orientation of the molecule. The interchangeable parts are said to be equivalent to one another by symmetry.

Let us consider a trigonal bipyramidal molecule PF5.

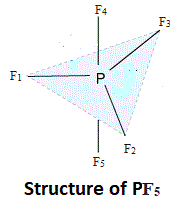
The three P – F bonds to F1, F2 and F3 are equivalent, same is the case for F4 and F5. Any permutations of these bonds among themselves leads to a molecule indistinguishable from the original, i.e., equivalent. But axial and equatorial bonds are different types and if one of these were interchanged, the molecule will be perturbed, i.e. not equivalent.

What is meant by symmetry operations?

A fundamental concept of the chemical application of group theory is the symmetry operation, an action, such as rotation through a certain angle, that leaves the molecule apparently unchanged.

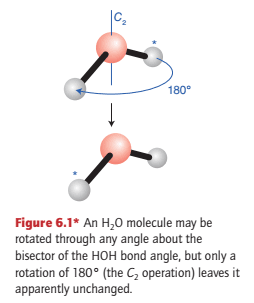
Symmetry operations are geometrically defined ways if exchanging equivalent parts of a molecule. An example is the rotation of an H2O molecule by 180° around the bisector of the HOH angle (Fig. 6.1).

Associated with each symmetry operation there is a symmetry element—a point, line, or plane with respect to which the symmetry operation is performed. All these operations leave at least one point unchanged and hence they are referred to as the operations of point-group symmetry.

Types of symmetry operations

The table lists the most important symmetry operations and their corresponding elements.

What is identity symmetry operations?

The identity operation, E, consists of doing nothing to the molecule. Every molecule has at least this operation and some have only this operation, so we need it if we are to classify all molecules according to their symmetry.

The rotation of an H2O molecule by 180° around a line bisecting the HOH angle (as in Fig. 6.1) is a symmetry operation, denoted C2.

In general, an n-fold rotation is a symmetry operation if the molecule appears unchanged after rotation by 360°/n. The corresponding symmetry element is a line, an n-fold rotation axis, Cn, about which the rotation is performed.

There is only one rotation operation associated with a C2 axis (as in H2O) because clockwise and anticlockwise rotations by 180° are identical.

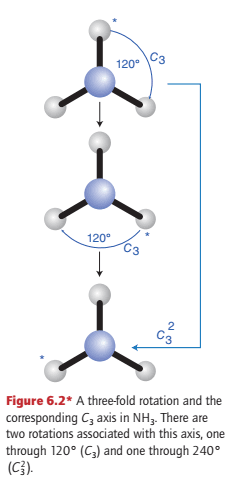
The trigonal-pyramidal NH3 molecule has a three-fold rotation axis, denoted C3, but there are now two operations associated with this axis, one a clockwise rotation by 120° and the other an anticlockwise rotation by 120° (Fig. 6.2). The two operations are denoted C3 and C32 (because two successive clockwise rotations by 120° are equivalent to an anticlockwise rotation by 120°), respectively.

The square-planar molecule XeF4 has a four-fold axis, C4, but in addition it also has two pairs of two-fold rotation axes that are perpendicular to the C4 axis: one pair (C2′) passes through each trans-FXeF unit and the other pair (C2′′) passes through the bisectors of the FXeF angles (Fig. 6.3).

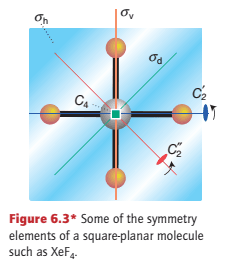
By convention, the highest order rotational axis, which is called the principal axis, defines the z-axis (and is typically drawn vertically). The C42 operation is equivalent to a C2 rotation, and this is normally listed separately from the C4 operation as ‘C2 = (C42)’.

How do you explain reflection symmetry operation?

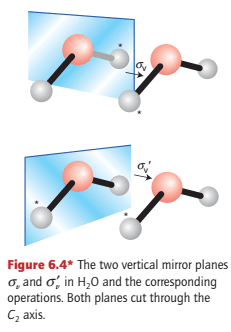
The reflection of an H2O molecule in either of the two planes shown in Fig. 6.4 is a symmetry operation; the corresponding symmetry element is a mirror plane, σ. The H2O molecule has two mirror planes that intersect at the bisector of the HOH angle. Because the planes are ‘vertical’, in the sense of containing the rotational (z) axis of the molecule, they are labelled with a subscript v, as in σv and σv′.

The XeF4 molecule in Fig. 6.3 has a mirror plane σh in the plane of the molecule. The subscript h signifies that the plane is ‘horizontal’ in the sense that the vertical principal rotational axis of the molecule is perpendicular to it.

This molecule also has two more sets of two mirror planes that intersect the four-fold axis. The symmetry elements (and the associated operations) are denoted σv for the planes that pass through the F atoms and σd for the planes that bisect the angle between the F atoms. The d denotes ‘dihedral’ and signifies that the plane bisects the angle between two C2′ axes (the FXeF axes).

What is an inversion symmetry operation?

To understand the inversion operation, i, we need to imagine that each atom is projected in a straight line through a single point located at the centre of the molecule and then out to an equal distance on the other side (Fig. 6.5).

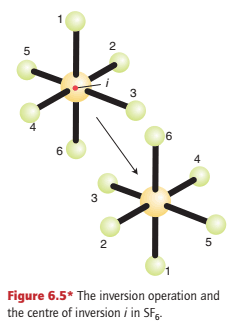
In an octahedral molecule such as SF6, with the point at the centre of the molecule, diametrically opposite pairs of atoms at the corners of the octahedron are interchanged. In general, under inversion, an atom with coordinates (x, y, z) moves to (-x, -y, -z). The symmetry element, the point through which the projections are made, is called the centre of inversion, i.

For SF6, the centre of inversion lies at the nucleus of the S atom. Likewise, the molecule CO2 has an inversion centre at the C nucleus.

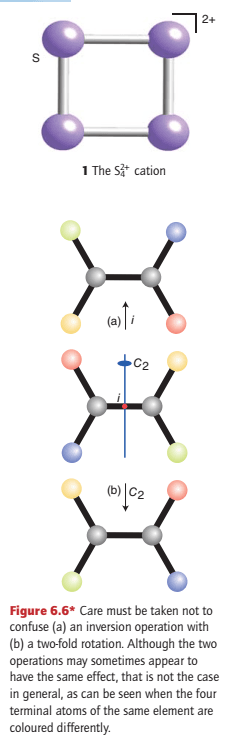
However, there need not be an atom at the centre of inversion: an N2 molecule has a centre of inversion midway between the two nitrogen nuclei and the S42+ ion (1) has a centre of inversion in the middle of the square ion.

An H2O molecule does not possess a centre of inversion, and no tetrahedral molecule can have a centre of inversion. Although an inversion and a two-fold rotation may sometimes achieve the same effect, that is not the case in general and the two operations must be distinguished (Fig. 6.6).

What is an improper rotation?

An improper rotation consists of a rotation of the molecule through a certain angle around an axis followed by a reflection in the plane perpendicular to that axis (Fig. 6.7).

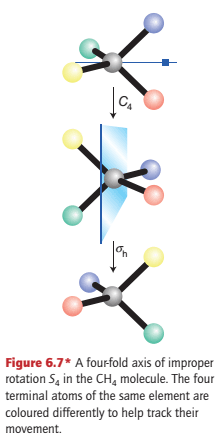
The illustration shows a four-fold improper rotation of a CH4 molecule. In this case, the operation consists of a 90° (that is, 360°/4) rotation about an axis bisecting two HCH bond angles, followed by a reflection through a plane perpendicular to the rotation axis.

Neither the 90° (C4) operation nor the reflection alone is a symmetry operation for CH4 but their overall effect is a symmetry operation. A four-fold improper rotation is denoted S4.

The symmetry element, the improper-rotation axis, Sn (S4 in the example), is the corresponding combination of an n-fold rotational axis and a perpendicular mirror plane.